这是一篇译文,原文地址:Top 10 Algorithms for Coding Interview
以下列出的是程序员面试中流行的算法概念。完全理解这些算法概念需要花更多的精力,所以本文只是对算法概念进行介绍。
1) String / Array 2) Matrix 3) Linked List 4) Tree / Heap
5) Graph 6) Sorting 7) Recursion / Iteration 8) Dynamic Programming
9) Bit Manipulation 10) Combinations / Permutations 11) Math Problems
如果你需要了解Java的基础知识,我十分建议你阅读 “Simple Java“。如果你想要知道使用一个流行的API的具体实例,你可以在 JavaSED.com 找到。
说明:在例题中,类似的问题用相同的数字标注。
1. String / Array
字符串是Java中的类。它包括了一个字符区域、其它区域和方法。如果你的 IDE 没有代码自动补全功能,你应当记住以下的方法:
toCharArray() //get char array of a String
charAt(int x) //get a char at the specific index
length() //string length
length //array size
substring(int beginIndex)
substring(int beginIndex, int endIndex)
Integer.valueOf() //string to integer
String.valueOf() //integer to string
Arrays.sort() //sort an array
Arrays.toString(char[] a) //convert to string
Arrays.copyOf(T[] original, int newLength)
System.arraycopy(Object src, int srcPos, Object dest, int destPos, int length)
字符串 / 数组的数据结构很容易理解,所以面试题中经常会需要用到高级的算法进行解决,例如动态规划,递归 等等。
经典问题如下:
1) Rotate Array - 字符串旋转
2) Evaluate Reverse Polish Notation (Stack) - 逆波兰式计算结果
3) Isomorphic Strings - 同型字符串
4) Word Ladder (BFS) - 单词梯子
4) Word Ladder II (BFS) - 单词梯子2
5) Median of Two Sorted Arrays - 找两个有序数组的中位数
5) Kth Largest Element in an Array - 找第K大的数
6) Wildcard Matching - 通配符比对
6) Regular Expression Matching - 正则表达式比对
7) Merge Intervals - 合并间隔段
8) Insert Interval - 插入间隔段
9) Two Sum II – Input array is sorted
9) Two Sum III - Data structure design
9) 3Sum
9) 4Sum
10) 3Sum Closest
11) String to Integer
12) Merge Sorted Array
13) Valid Parentheses
13) Longest Valid Parentheses
14) Implement strStr()
15) Minimum Size Subarray Sum
16) Search Insert Position
17) Longest Consecutive Sequence
18) Valid Palindrome
19) ZigZag Conversion
20) Add Binary
21) Length of Last Word
22) Triangle
24) Contains Duplicate
24) Contains Duplicate II
24) Contains Duplicate III
25) Remove Duplicates from Sorted Array
26) Remove Duplicates from Sorted Array II
27) Longest Substring Without Repeating Characters
28) Longest Substring that contains 2 unique characters [Google]
28) Substring with Concatenation of All Words
29) Minimum Window Substring
30) Reverse Words in a String
31) Find Minimum in Rotated Sorted Array
31) Find Minimum in Rotated Sorted Array II
31) Search in Rotated Sorted Array
31) Search in Rotated Sorted Array II
32) Find Peak Element
33) Min Stack
34) Majority Element
34) Majority Element II
35) Remove Element
36) Largest Rectangle in Histogram
37) Longest Common Prefix [Google]
38) Largest Number
39) Simplify Path
40) Compare Version Numbers
41) Gas Station
44) Pascal’s Triangle
44) Pascal’s Triangle II
45) Container With Most Water
45) Candy [Google]
45) Trapping Rain Water
46) Count and Say
47) Search for a Range
48) Basic Calculator
49) Anagrams
50) Shortest Palindrome
51) Rectangle Area
52) Summary Ranges
2. Matrix
经常用来解决矩阵相关问题的算法包括 DFS,BFS,动态规划 等等。
经典问题如下:
1) Set Matrix Zeroes
2) Spiral Matrix
2) Spiral Matrix II
3) Search a 2D Matrix
4) Rotate Image [Palantir]
5) Valid Sudoku
6) Minimum Path Sum (DP) [Google]
7) Unique Paths (DP) [Google]
7) Unique Paths II (DP)
8) Number of Islands (DFS/BFS)
9) Surrounded Regions (BFS)
10) Maximal Rectangle
10) Maximal Square
11) Word Search (DFS)
11) Word Search II
3. Linked List
Java 中链表的实现十分简单。每个节点有个值和一个指向下一个节点的链接。
class Node {
int val;
Node next;
Node(int x) {
val = x;
next =null;
}
}两种链表的普遍应用是栈和队列。
Stack
class Stack {
Node top;
public Node peek() {
if(top !=null) { return top; }
return null;
}
public Node pop() {
if(top == null) { return null; }
else {
Node temp = new Node(top.val);
top = top.next;
return temp;
}
}
public void push(Node n) {
if(n !=null) {
n.next= top;
top = n;
}
}
}Queue
class Queue {
Node first, last;
public void enqueue(Node n) {
if(first == null) {
first = n;
last = first;
} else {
last.next= n;
last = n;
}
}
public Node dequeue() {
if(first == null) {
return null;
} else {
Node temp = new Node(first.val);
first = first.next;
return temp;
}
}
}Java 标准库中有一个类叫做 “Stack“。在 Java SDK 中还有一个类叫做 “Linked List“,可以被当做队列使用,具有 add() 和 remove() 方法。(Linked List 实现了 Queue 的接口)。记得在面试中适时地使用栈和队列。
经典问题如下:
1) Add Two Numbers
2) Reorder List
3) Linked List Cycle
4) Copy List with Random Pointer
5) Merge Two Sorted Lists
6) Merge k Sorted Lists *
7) Remove Duplicates from Sorted List
7) Remove Duplicates from Sorted List II
8) Partition List
9) LRU Cache
10) Intersection of Two Linked Lists
11) Remove Linked List Elements
12) Swap Nodes in Pairs
13) Reverse Linked List
13) Reverse Linked List II
14) Remove Nth Node From End of List (Fast-Slow Pointers)
15) Implement Stack using Queues
15) Implement Queue using Stacks
16) Palindrome Linked List
17) Implement a Queue using an Array
18) Delete Node in a Linked List
4. Tree / Heap
树结构,通常是指二叉树。每个节点有一个左节点和右节点,如下所示:
class TreeNode {
int value;
TreeNode left;
TreeNode right;
}与二叉树相关的概念:
- 二叉搜索树:对于所有的节点,都有 左子节点<=当前节点<=右子节点
- 平衡树:左子树和右子树的高度相差小于等于1
- 满二叉树:除了叶子节点外,所有的节点都有两个子节点
- 完美二叉树:首先使一个满二叉树,其次,所有的叶子节点都有相同的深度,或者在同一级,而且,叶子节点的父节点都有两个子节点
- 完全二叉树:除了最后一级外,其余层级都被填满了,另外,所有节点都靠左排列
Heap(堆) 是一个满足堆属性的,基于树结构的数据结构。对于堆操作来说,时间复杂性是重要的(例如:查找最小值,删除最小值,插入 等等)。在 Java 语言中,Priority Queue(优先队列) 也是值得了解的。
经典问题如下:
1) Binary Tree Preorder Traversal
2) Binary Tree Inorder Traversal [Palantir]
3) Binary Tree Postorder Traversal
4) Binary Tree Level Order Traversal
4) Binary Tree Level Order Traversal II
5) Validate Binary Search Tree
6) Flatten Binary Tree to Linked List
7) Path Sum (DFS or BFS)
7) Path Sum II (DFS)
8) Construct Binary Tree from Inorder and Postorder Traversal
8) Construct Binary Tree from Preorder and Inorder Traversal
9) Convert Sorted Array to Binary Search Tree [Google]
10) Convert Sorted List to Binary Search Tree [Google]
11) Minimum Depth of Binary Tree
12) Binary Tree Maximum Path Sum *
13) Balanced Binary Tree
14) Symmetric Tree
15) Binary Search Tree Iterator
16) Binary Tree Right Side View
17) Implement Trie (Prefix Tree)
18) Add and Search Word - Data structure design (DFS)
19) Merge k sorted arrays [Google]
20) Populating Next Right Pointers in Each Node
21) Populating Next Right Pointers in Each Node II
21) Unique Binary Search Trees (DP)
21) Unique Binary Search Trees II (DFS)
22) Sum Root to Leaf Numbers (DFS)
23) Count Complete Tree Nodes
24) Invert Binary Tree
25) Kth Smallest Element in a BST
26) Lowest Common Ancestor of a Binary Search Tree
26) Lowest Common Ancestor of a Binary Tree
5. Graph
图相关的问题,主要用深度优先搜索和宽度优先搜索来解决。深度优先搜索,顾名思义,你可以从根节点开始,循环地访问它的邻居节点。
下图是宽度优先搜索的简单实现的示例图。关键之处在于使用一个队列来存储节点。
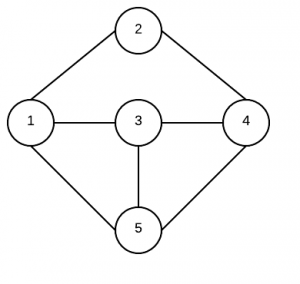
1) 定义图的节点
class GraphNode {
int val;
GraphNode next;
GraphNode[] neighbors;
boolean visited;
GraphNode(int x) {
val = x;
}
GraphNode(int x, GraphNode[] n) {
val = x;
neighbors = n;
}
public String toString() {
return"value: " + this.val;
}
}2) 定义队列
class Queue {
GraphNode first, last;
public void enqueue(GraphNode n) {
if(first ==null) {
first = n;
last = first;
} else {
last.next= n;
last = n;
}
}
public GraphNode dequeue() {
if(first == null) {
returnnull;
} else {
GraphNode temp = new GraphNode(first.val, first.neighbors);
first = first.next;
return temp;
}
}
}3) 使用队列进行BFS
public class GraphTest {
public static void main(String[] args) {
GraphNode n1 =new GraphNode(1);
GraphNode n2 =new GraphNode(2);
GraphNode n3 =new GraphNode(3);
GraphNode n4 =new GraphNode(4);
GraphNode n5 =new GraphNode(5);
n1.neighbors=new GraphNode[]{n2,n3,n5};
n2.neighbors=new GraphNode[]{n1,n4};
n3.neighbors=new GraphNode[]{n1,n4,n5};
n4.neighbors=new GraphNode[]{n2,n3,n5};
n5.neighbors=new GraphNode[]{n1,n3,n4};
breathFirstSearch(n1, 5);
}
public static void breathFirstSearch(GraphNode root, int x) {
if(root.val== x)
System.out.println("find in root");
Queue queue =new Queue();
root.visited=true;
queue.enqueue(root);
while(queue.first != null) {
GraphNode c =(GraphNode) queue.dequeue();
for(GraphNode n : c.neighbors) {
if(!n.visited) {
System.out.print(n +" ");
n.visited=true;
if(n.val== x)
System.out.println("Find "+n);
queue.enqueue(n);
}
}
}
}
}输出:
value: 2 value: 3 value: 5 Find value: 5
value: 4
经典问题如下:
1) Clone Graph
2) Course Schedule (BFS/DFS)
2) Course Schedule II (BFS)
6. Sorting
以下列出若干排序算法的时间复杂度。你可以自行了解排序算法的具体概念。
| 算法 | 平均时间 | 最差情况 | 所需空间 |
|---|---|---|---|
| 冒泡排序 | n^2 | n^2 | 1 |
| 选择排序 | n^2 | n^2 | 1 |
| 插入排序 | n^2 | n^2 | |
| 快速排序 | n*log(n) | n^2 | |
| 合并排序 | n*log(n) | n*log(n) | 看情况 |
说明:桶排序、基数排序和计数排序 基于与上述排序方法不同的前提,它们属于“非一般”的排序算法,故没有罗列。
以下是一些实现方式和示例程序。另外,有兴趣的话可以参考 “Java developers sort in practice“。
1) Mergesort
2) Quicksort
3) InsertionSort
4) Maximum Gap (Bucket Sort)
5) First Missing Positive (Bucket Sort)
6) Sort Colors (Counting Sort) Sort Colors (Counting Sort))
7. Recursion / Iteration
对程序员来说,递归是应该具有的思想(a built-in thought)。
问题:有n步台阶,一次只能上1步或2步,问共有多少种走法。
Step 1: 找出走完前n步台阶和前n-1步台阶之间的关系
为了走完n步台阶,只有两种方法:从n-1步台阶爬1步走到或从n-2步台阶处爬2步走到。如果f(n)是爬到第n步台阶的方法数,那么f(n) = f(n-1) + f(n-2)
Step 2: 确保开始条件是正确的
f(0) = 0;
f(1) = 1;
函数如下:
public static int f(int n) {
if(n <=2)
return n;
int x = f(n-1)+ f(n-2);
return x;
}递归方法的时间复杂度是 n 的指数级,递归过程如下:
f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(2) + f(2) + f(1)
将递归转换为迭代:
public static int f(int n) {
if(n <= 2) {
return n;
}
int first = 1, second = 2;
int third = 0;
for(int i = 3; i <= n; i++) {
third = first + second;
first = second;
second = third;
}
return third;
}8. Dynamic Programming
动态规划用来解决具有如下属性的问题:
- 一个问题可以通过更小子问题的解决方法来解决。
- 有些子问题的解可能需要计算多次。
- 子问题的解存储在一张表格里,这样每个子问题只用计算一次。
- 需要额外的空间以节省时间。
递归和迭代章节 的走台阶问题,符合以上4条特性,可以使用动态规划来解决。
public static int[] A = new int[100];
public static int f3(int n) {
if(n <= 2)
A[n] = n;
if(A[n] > 0)
return A[n];
else
A[n]= f3(n-1) + f3(n-2); //store results so only calculate once!
return A[n];
}经典问题如下:
1) Edit Distance
1) Distinct Subsequences Total
2) Longest Palindromic Substring
3) Word Break
3) Word Break II
4) Maximum Subarray
4) Maximum Product Subarray
5) Palindrome Partitioning
5) Palindrome Partitioning II
6) House Robber [Google]
6) House Robber II
7) Jump Game
7) Jump Game II
8) Best Time to Buy and Sell Stock
8) Best Time to Buy and Sell Stock II
8) Best Time to Buy and Sell Stock III
8) Best Time to Buy and Sell Stock IV
9) Dungeon Game
10) Minimum Path Sum
11) Unique Paths
12) Decode Ways
9. Bit Manipulation
位操作符:
OR (|) |
AND (&) |
XOR (^) |
Left Shift (<<) |
Right Shift (>>) |
Not (~) |
1|0 = 1 |
1&0 = 0 |
1^0 = 1 |
0010<<2 = 1000 |
1100>>2 = 0010 |
~1 = 0 |
问题:给定一个正整数n,求它的第 i 位。(i 从0开始,并从右往左计)
public static boolean getBit(int num, int i) {
int result = num &(1<<i);
if(result ==0) {
return false;
} else {
return true;
}
}例如,获取 10 的第 2 位的过程如下:
i=1, n=10
1<<1= 10 1010&10=10 10 is not 0, so return true;
经典问题如下:
1) Single Number
1) Single Number II
2) Maximum Binary Gap
3) Number of 1 Bits
4) Reverse Bits
5) Repeated DNA Sequences
6) Bitwise AND of Numbers Range
7) Power of Two
10. Combinations and Permutations
组合和排列的区别在于,顺序是否要考虑在内。
比如下面两个问题:
问题1:给出1,2,3,4 和 5,打印出这5个数的不同序列。要求:4 不能是第三个;3 和 5 不能相邻。问有多少种不同的组合?
问题2: 有5个香蕉,4个梨和3个苹果,假设同一种类的水果都是相同的,请问有多少种不同的组合?
经典问题如下:
1) Permutations
2) Permutations II
3) Permutation Sequence
4) Generate Parentheses
5) Combination Sum (DFS)
5) Combination Sum II (DFS)
5) Combination Sum III (DFS)
6) Combinations (DFS)
7) Letter Combinations of a Phone Number (DFS)
8) Restore IP Addresses
11. Math Problems
解决数学问题,通常需要观察问题,然后总结出规律。
经典问题如下:
1) Reverse Integer
2) Palindrome Number
3) Pow(x,n)
4) Subsets
5) Subsets II
6) Fraction to Recurring Decimal [Google]
7) Excel Sheet Column Number
8) Excel Sheet Column Title
9) Factorial Trailing Zeroes
10) Happy Number
11) Count Primes
12) Plus One
13) Divide Two Integers
14) Multiply Strings
15) Max Points on a Line
16) Product of Array Except Self
This work is licensed under a CC A-S 4.0 International License.